CSE 40657/60657
Homework 2

Setup

Clone the Homework 2 repository. It contains the following files:

The data is the text of Hamlet from Shakespeare's First Folio in original and modern English spelling. The training data is everything up to where Hamlet dies (spoiler alert) and the test data is the last 50 or so lines afterwards.

The fst module should be extremely helpful for this assignment. If you're writing in a language other than Python, please talk to the instructor about getting equivalent help in your programming language.

In the following, point values are written after each requirement, like this.30

1. Building blocks

1. Construct a weighted FST $M_{\text{LM}}$ for a bigram language model for modern English and train it on train.new.1 Feel free to reuse code from HW1, or someone else's code or the official solution's code, as long as you cite it. Smoothing shouldn't be necessary.
2. Write code to construct an unweighted FST $M_{\text{TM}}$ that transforms strings over the modern alphabet into strings over the original alphabet.5 It should allow substitutions, insertions, and at most one deletion as discussed in class. You can view your FST in a Jupyter notebook and check that it looks something like this (shown here for a two-letter alphabet): 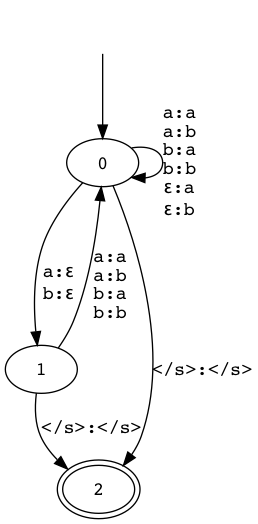Yours should be able to input any character found in train.new and output any character found in train.old.
3. Write code that takes a string $w$ and creates an unweighted FST $M_w$ that inputs just $w \texttt{</s>}$ and outputs just $w \texttt{</s>}$.1 Again, you can view your FST in a Jupyter notebook to check it. (The function fst.string pretty much does htis for you.)

2. Decoding

1. Initialize the probabilities of $M_{\text{TM}}$. Since we know that most letters in original spelling stay the same in modern spelling, give transitions on $a:a$ more probability (like 100 times more); this makes it easier to know if your decoder is working. To ensure that probabilities correctly sum to one, you can set the transition counts to whatever you want, and then use fst.estimate_cond() to compute probabilities from them. Briefly describe your initialization.1
2. For each original line $w$ in the test set, use fst.compose() to compose $M_{\text{LM}}$, $M_{\text{TM}}$, and $M_w$.1
3. Implement the Viterbi algorithm to find the best path through this FST.5 Be sure to visit the states in the correct order. We provide a function fst.topological_sort to give you a correct ordering. The notes (page 36) have been updated with a slight variant of the algorithm that is better suited to our data structures.
4. Run your Viterbi algorithm on test.old. For the first ten lines, report the best modernization together with its log-probability:

   [Horatio] Now cracke a Noble heart.     -108.6678162110888
   Good ight sweet Prince,                 -85.19153221166528
   

   and so on.1
5. Use the cer module to evaluate how well your modernizer works. You can either call cer.cer() directly as a function, or run cer.py test.new youroutput.new where youroutput.new is a file containing your outputs. (Don't forget to remove the log-probabilities.) Report your score.1 A lower score is better; if you initialize the model well, you should get a score under 10%.1

3. Training (CSE 40657/60657 only)

This part is optional for CDT 40310 students, who automatically get full credit.

Now, we'll improve our modernizer by training the model using hard EM. We'll train on parallel text rather than on nonparallel text as in class; it's faster this way and gives better results.

1. Implement the E step: For each line in the training data, consisting of a modern string $m$ and an original string $e$,
   • Compose $M_m$, $M_{\text{TM}}$, and $M_e$.1 Note that this is different from Part 2.
   • Use the Viterbi algorithm to find the best path through the composed transducer.1
   • Now count how many times each transition of $M_{\text{TM}}$ was used in that best path.4 That is, every transition in the composed transducer is made from (possibly) a transition of $M_m$, a transition of $M_{\text{TM}}$, and (possibly) a transition of $M_e$. For each transition t of $M_{\text{TM}}$, how many times does the best path use a transition that is made from t? Note that fst.compose keeps track of which transitions are made from which: when you do m = fst.compose(m1, m2), for each transition t created, m.composed_from[t] is the pair of transitions that t was made from.
   • Accumulate those counts over all the lines in the training data.1
2. Implement the (rest of the) M step: Renormalize the counts collected above to reestimate the transition probabilities of $M_{\text{TM}}$.1 It's pretty important to apply some add-$\delta$ smoothing at this point. The method FST.normalize_cond() fst.estimate_cond takes an optional parameter add that lets you do this.
3. Repeat the above steps for a few iterations. After each iteration,
   • Decode test.old and measure your score against test.new. Report your score.1 It should eventually get better than 7.5%.1
   • Print your outputs for the first ten lines.1
   • Print the probabilities of all transition weights greater than or equal to 0.1.1
4. Briefly describe what you saw your model learn.1

Submission

Please submit all of the following in a gzipped tar archive (.tar.gz or .tgz; not .zip or .rar) via Sakai:

• A PDF file (not .doc or .docx) with your responses to the instructions/questions above.
• All of the code that you wrote.
• A README file with instructions on how to build and run your code on student*.cse.nd.edu. If this is not possible, please discuss with the instructor before submitting.