Homework 1: Scheme and induction

Due: 01/25 at 11:55pm
Points: 15 (each question 5 points)

Please prepare your solution for problem 1 as a .scm file and your answers to problems 2-3 as a PDF file (scanned handwriting is okay, but no .doc or .docx, please). Submit both files in Sakai.

1. Caesar ciphers

This exercise is a refresher in Scheme, particularly in using higher-order functions and lexical scoping.

The Caesar cipher was used by Julius Caesar to encrypt his private letters (Suetonius Vita Divi Iulii 56.6). A Caesar cipher with a shift of k replaces the i’th letter of the alphabet with the (i + k)’th letter of the alphabet (mod 26). For example, a Caesar cipher with a shift of −3 would change ECCE to BZZB. In this problem, you’ll implement this cipher in Scheme.

Install Guile. On student0x.cse.nd.edu, it’s installed at ~dchiang/Public/guile/bin/guile. To enable editing and history, create a file called ~/.guile with the expressions
```
(use-modules (ice-9 readline))
(activate-readline)
```
Write a function called caesar that takes no arguments. It should choose a random number k between 1 and 25 (inclusive) and return a pair (cons) of functions, one which encodes strings with a shift of k and one which decodes strings with the same shift. Assume that strings use only uppercase letters. For example,
```
> (let ((encdec (caesar)))
    (let ((encode (car encdec))
          (decode (cdr encdec)))
      (encode "ECCE")))
"YWWY"
```
(but since the shift is random, you might get a different result). And encoding then decoding should yield the original string:
```
> (let ((encdec (caesar)))
    (let ((encode (car encdec))
          (decode (cdr encdec)))
      (decode (encode "ECCE"))))
"ECCE"
```
It should be possible to create multiple encoder/decoder pairs at the same time. (In other words, don’t store k in a global variable.)
Try to make your encoder and decoder run in O(1) space. It’s not a requirement, but it’s good functional programming practice.
The following Scheme functions should be handy:
- (random n) gives a random integer between 0 and n − 1 inclusive. (This function is part of Guile; other Schemes might be different.)
- (modulo n m) is the same as Python’s % operator. (It behaves differently from C/C++’s % for negative numbers.)
- string->list and list->string convert strings to lists of characters and vice versa.
- char->integer and integer->char convert characters to integers and vice versa. Note that the letter A converts to 65.

2. Red-black trees: definition

This exercise and the next are for practicing the style of inductive definitions and proofs used throughout the book.

Here’s a definition of binary trees with nodes that are colored either red or black:

t₁ bintree   t₂ bintree
———————————————————————   c ∈ {red,blk}
    c(t₁,t₂) bintree

       —————————          c ∈ {red,blk}
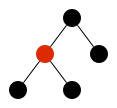
       c bintree

This definition represents trees as terms. For example, the tree in Figure 1 is represented as blk(red(blk,blk),blk).

Modify the above definition into a definition of the judgement t rbtree that holds iff the colors satisfy the rules for red-black trees:

The root is black.
The leaves are black.
If a node is red, then both its children are black.
For each node, there is a number b (called its black-height) such that every path from the node to a leaf has exactly b black nodes.

Hint: First define the judgement t rbtree(c,b), which holds iff t is a red-black tree with root color c and black-height b. (For this “helper” judgement, we suspend the requirement that the root is black.) Then define t rbtree in terms of t rbtree(c,b).

Write a derivation tree that shows that the tree shown in Figure 1 is a red-black tree.

3. Red-black trees: height bound

Define the height of a tree to be the maximum number of edges in a path from root to leaf. (Yes, it’s strange that black-height counts nodes but height counts edges.) You learned in Data Structures, but may not have proven, that the height of a red-black tree is O(log n), which makes them good for implementing dictionaries.

Prove, by induction(s) on the structure of derivations, that a red-black tree with n nodes has height at most 2 log₂(n + 1) − 2. Hint: Do this in three steps:

Prove that if t rbtree(c,b), then t has n ≥ 2^b − 1 nodes.
Prove that if t rbtree(c,b), then t has height h ≤ 2b − 1 if c is red, and h ≤ 2b − 2 if c is black.
Conclude that h ≤ 2 log₂(n + 1) − 2.

Note: This is the last time you will see a logarithm in this class!