Homework 2: Untyped λ-calculus

• Due: 02/08 at 11:55pm
• Points: 15 (each question 5 points)

Please prepare your solutions as a PDF file (scanned handwriting is okay, but no .doc or .docx, please). If you prefer, you can write your solutions to problems 2-3 as plain text files. Submit all files in Sakai.

1. Lambda calculations

Prove each of the following statements. If the statement is of the form t ⟶* t', show each call-by-value β-reduction step with the redex underlined. If the statement is of the form t = t', find a third term t" such that t ⟶v* t" and t' ⟶v* t", and prove both, showing each βᵥ-reduction step with the redex underlined.

For example:

    (λx. x) (λy. y) (λz. z)
    ―――――――――――――――

⟶ (λy. y) (λz. z)
    ―――――――――――――――

⟶ (λz. z)

1. (λx. λx. x) (λy. λz. y) (λy. λz. z) ⟶* λy. λz. z
2. (λx. λy. y x) (y y) z ⟶* z (y y)
3. (λx. λy. λz. x z (y z)) (λx. λy. x) (λx. λy. x) = λz. z
4. (λm. λn. λs. λz. m s (n s z)) x (λs. λz. z) = (λm. λn. λs. λz. m s (n s z)) (λs. λz. z) x

2. Church trees

Added explanation: In this problem, we’ll explore how to represent binary trees (without labels) as λ-terms. Just as the Church numeral for a number is a function of two arguments, s and z, that applies s to z that number of times, we want to represent a tree as a function of two arguments, n and l, that applies n to l in the same “shape” as the tree. For example, the tree below is represented by λn. λl. n (n l l) l.

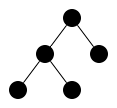
1. Write λ-terms leaf and node that satisfy the following:

         leaf n l = l
   node t1 t2 n l = n (t1 n l) (t2 n l)

   (There’s almost nothing to do here.) The term leaf is a tree consisting of just one leaf; the term node t1 t2 is a tree consisting of a root node with t1 and t2 as its child subtrees. Added: For example, the tree above can be constructed by node (node leaf leaf) leaf.

2. Write a λ-term isleaf that tells whether a tree’s root is a leaf node. For example,

               isleaf leaf = true
   isleaf (node leaf leaf) = false

3. Write a λ-term size that counts the number of nodes (including leaves) in a tree (as a Church numeral). For example, node leaf leaf has three nodes, so size (node leaf leaf) = c3.

4. Challenge (0 points): Write λ-terms left and right that return the left and right child subtrees, respectively, of a tree’s root. That is, they should satisfy:

    left (node t1 t2) = t1
    left  leaf        = leaf
   right (node t1 t2) = t2
   right  leaf        = leaf

3. Hailstone sequences

The hailstone sequence starting with n is defined as follows:

• a₀ = n.
• If a_n is even, a_n + 1 = n/2.
• If a_n is odd, a_n + 1 = 3n + 1.

The Collatz conjecture is that for all n > 0, the hailstone sequence starting with n eventually reaches 1.

1. Write a λ-term that, given the Church numeral for n > 0, returns tru if the hailstone sequence starting with n eventually reaches 1; otherwise, it diverges.

   You may assume that you have a function divmod such that for any Church numerals x and y, divmod x y is a pair containing the quotient and remainder of x divided by y.

2. Challenge (0 points): Write divmod too.