How is circuit analysis performed?

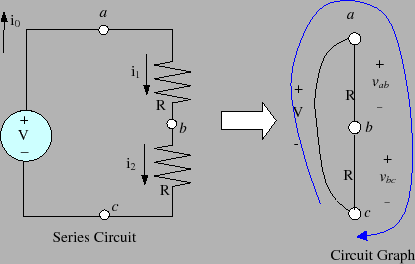
As was mentioned earlier, a circuit is an interconnection of electrical devices. For the most part, we'll be concerned with interconnections of two-terminal devices such as resistors and diodes. An example of such a circuit is shown below in figure 9. The lefthand picture is the circuit diagram and the righthand picture is the circuit's graph.

Figure 9: A Simple Circuit

Circuit analysis requires that we determine the voltage across and current through all branches of a circuit. For the circuit in figure 9, the independent voltage source makes it easy to specify the voltage across nodes $a$ and $b$, but how do we analyze the rest of the circuit? To do this, we need to invoke two special physical laws that lie at the heart of all circuit analysis. In particular, we need to use the laws known as Kirchoff's current law or KCL and Kirchoff's voltage law KVL. These two laws are conservation principles that must always be obeyed by any passive circuit. We can use these laws to help determine the voltages and currents in the circuit's branches.

Kirchoff's Voltage Law (KVL) is stated with respect to a loop in a circuit's graph. It states that: `` the algebraic sum of the voltages around any loop equals zero. `` A loop is a sequence of connected branches that begin and end at the same node. Figure 9 marks one of the loops in our circuit. This is the loop formed from branches

$$\begin{eqnarray*} (a,b) \rightarrow (b,c) \rightarrow (c,a) \end{eqnarray*}$$

The voltages obtained by traversing this loop are

$$\begin{eqnarray*} v_{ab}, v_{bc}, V \end{eqnarray*}$$

KVL says that the "algebraic" sum of these voltages must equal zero. By algebraic, we mean that the voltages are signed quantities. The voltage polarity or sign of each arc is determined by the direction in which we traverse the arc. If we start at node $a$ and begin tracing out our loop in a clockwise direction, we see that the traverse of branch $(a,b)$ goes from $+$ to $-$. This is considered as a negative change in potential (i.e. we're decreasing the potential). The same is true for the voltage over branch $(b,c)$. Note, however, that in traversing branch $(c,a)$ that we are going from a negative to positive polarity. The change in potential, therefore, is positive. On the basis of our preceding discussion, we can see that KVL will lead to the following equation:

$$\begin{eqnarray*} V - v_{ab} - v_{bc} = 0 \end{eqnarray*}$$

KVL is an energy conservation relation. It states, in essence, that the total work done in going around a loop will be zero.

The other important circuit relation is Kirchoff's current law. Kirchoff's Current Law (KCL) is stated as follows: `` The algebraic sum of current at any node is zero. `` To explain what this statement means, let's consider the circuit shown in figure 10. This figure shows an independent source of $V$ volts connected to a resistive network . The single node $a$ of this circuit is shown in the righthand drawing of figure 10. At this node, we see three currents. Two of these currents $i_1$ and $i_2$ are leaving node $a$ and the third current $i_0$ is entering node $a$. Currents that are entering a node are assumed to have a positive sign, whereas currents leaving a node have a negative sign. By Kirchoff's current law, the algebraic sum (which takes into account the sign of the currents) must be zero. This means, therefore, that

$$\begin{eqnarray*} i_0-i_1 - i_2 = 0 \end{eqnarray*}$$

Note in this equation that the sign preceding current $i_1$ and $i_2$ is negative. This is because those currents are leaving node $a$ and therefore have a negative sense.

Figure 10: KCL at node $b$

Kirchoff's current law is simply a statement that charge cannot accumulate at the nodes of a circuit. This actually makes quite a bit of sense if you realize that the nodes are perfect conductors and therefore provide no place for charges to rest. This principle is identical to concepts found in fluid dynamics. Namely that if you look at the fluid flowing into one end of a pipe, you expect the same amount of fluid to flow out the other end. If this did not occur, then fluid would accumulate in the pipe and eventually cause the pipe to burst. KCL is nothing more than an electrical equivalent of this intuitive physical idea from fluid mechanics.

The key issue is to see how we can use KVL, KCL and Ohm's law to determine all of the branch voltages and currents in a specified circuit. We use the circuit in figure 9 to illustrate this process. What we will now do is determine all of the currents and voltages in this circuit.

We begin by using KCL at node $a$, $b$, and $c$. Remember that KCL states that the sum of the currents entering a node must equal the sum of the currents exiting a node. Applying KCL to nodes $a$, $b$, and $c$ will therefore result in three different equations

$$\begin{eqnarray*} i_0 &=& i_1 \\ i_1 &=& i_2 \\ i_2 &=& i_0 \end{eqnarray*}$$

These three equations, of course, simply say that the current going through all branches in the circuit must be equal. In other words, KCL allows us to conclude that $i_0 = i_1 = i_2$.

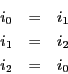
We now look at the voltages over each of the branches in this circuit. Because arc $(c,a)$ is an independent voltage source, we know that $v_{ac}=V$ volts. The other arcs, however, are resistors and this means that they must satisfy Ohm's law. Applying Ohm's law to these branches allows us to conclude that

$$\begin{eqnarray*} v_{ab} &=& i_1 R \\ v_{bc} &=& i_2 R \end{eqnarray*}$$

Note that we've already deduced that $i_1=i_2=i_0$, so that because the resistors have identical values of $R$ ohms, we can also conclude that $v_{ab}=v_{bc}= i_0 R$.

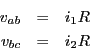
Finally, we use KVL (as before) to write down a single loop equation relating all of the voltages,

$$\begin{eqnarray*} V - v_{ab} - v_{bc} = 0 \end{eqnarray*}$$

Using our previous results, this equation can be rewritten as

$$\begin{eqnarray*} V- i_0 R - i_0 R =0 \end{eqnarray*}$$

which is an algebraic equation in a single unknown quantity $i_0$. We can now solve for $i_0$ to deduce that

$$\begin{eqnarray*} i_0 = \frac{V}{2R} \end{eqnarray*}$$

So we've determined the current leaving the voltage source $i_0$ as a function of $V$ (independent voltage source) and $R$ (the resistance).

On the way, however, we determined that all of the other currents and voltages in the circuit can be written as functions of this current $i_0$. Recall, that we deduced that $i_0=i_1=i_2 = V/2R$, so that we now know all of the currents in the circuit. Once the currents are known, we can use Ohm's Law to readily deduce that $v_{ab}=v_{bc}=V/2$. In other words, this circuit evenly divides the voltage supplied by the independent voltage source between the two resistors in the circuit.