CheckList 02

Overview

In addition to everything from Checklist 01, the final will cover the following topics:

Unit 4: Hash Tables
Unit 5: Graphs
Miscellaneous Topics
- Map-Reduce
- Bloom Filters

The final will consist of short answer and long answer questions.

Below are examples of the type of questions that may be asked on the midterm (many of them come from the exam last year). It is meant to be representative, rather than exhaustive (ie. there may be questions that show up on the midterm that are not shown below).

Comprehensive Final Exam

Although the final exam is comprehensive, it will mainly focus on the second half of the semester.

Short Answers

You need a data structure to represent a set of roughly 1 million objects, with random insertions, searches, and deletions. Give an example of a bad data structure for this job and a good data structure for this job. For each, explain in a few words why it is bad or good.
- Bad:
- Good:
Circle all of the following things that binary heaps (std::priority_queue) can be used for:
1. Sorting in O(n log n) time
2. Searching for a particular value in a set of values in O(log n) time
3. Searching for the k largest values in a set of values in O(n log k) time
4. Finding the shortest path between two nodes in a graph
What is the maximum ratio between the length of the longest root-to-leaf path and the shortest root-to-leaf path in each of the following data structures? Assume that the tree has n nodes.
- binary search tree:
- B-tree:
- red-black tree:
In a hash table with open addressing, if there is a collision, one way to find a new location is linear probing. Name another way and briefly describe what it does.
In a bucket sort, the function (h) that assigns items (x) to buckets must satisfy what property?
For each graph, determine if the graph is simple (yes or no):
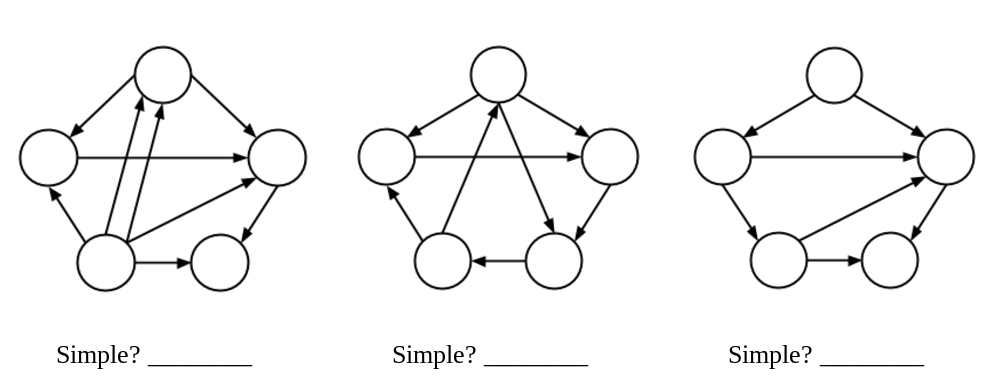
Assuming that every vertex has an edge to at least one other vertex in a graph G and starting from an arbitrary vertex v, circle all of the following statements about graph traversal that are true:
1. DFS from v will visit every node if G is an undirected graph.
2. BFS from v will visit every node if G is a directed graph.
3. Dijkstra's from v will not visit every node if G is directed and contains negative edge weights.
In a Bloom filter, how do the size of the table and the probability of error depend on k, the number of hash functions used? Use big-O notation, equations, or words.
- table size (this was called m in the notes, l in class):
- probability of error (e):

Suppose you build a large database, with 1 billion items in it. You find that linear search, binary search, and merge sort in this database take the amounts of time shown in the table below. Then, you expand the database to 1 trillion items. Estimate how long these three operations will take after the expansion. Explain your reasoning if necessary.

Operation	Before (1 Billion)	After (1 Trillion)
linear search	10 seconds
binary search	0.003 seconds
merge sort	3000 seconds

A binary heap is a complete binary tree which is typically stored in an array. Draw the tree that the following array represents:
```
[ 7 | 5 | 3 | 1 | 2 | 1 ]
```
If a node of the tree is at index i of the array, at what index is the node's:
- parent?
- left child?
- right child?
What is the best-case time complexity of inserting or searching in a hash table with separate chaining (big-O in terms of n, the number of elements in the hash table)? Explain under what conditions is this best-case achieved -- there's a condition on the hash function and a condition on the hash table.

If the hash function:

and the hash table:

then the time complexity of insertion/search is:
Starting with an empty hash table using [open addressing] (and linear probleing with an interval of 1), and using the hash function h(x) = x % 10, show the result of inserting the following values into the table:
```
7, 3, 2, 78, 56, 72, 79, 68, 13, 14
```
Bucket Value

0

1

2

3

4

5

6

7

8

9
In many real-world hash table implementations, the load factor is constrained to lie within some range, for example, between 1/2 and 3/4. Explain how the load factor impacts the performance (time and space) of both open addressing and separate chaining.
You need to store a graph that represents all of the college football games played during a regular season. Each node in the graph is a team, and each edge is a game. What would be an appropriate data structure for this graph? Briefly justify your answer. (Note: there are 128 teams in Division I FBS, and each team plays 12 or 13 games)
Given the following graph:

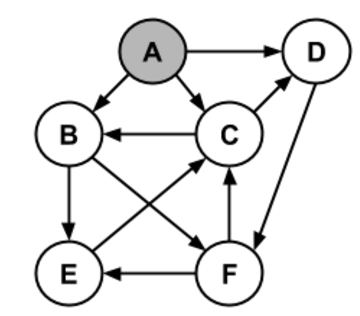
Write the order in which BFS would mark each node starting from A:

Do the same thing, using DFS:
Identify the three phases of a typical Map-Reduce workflow and briefly describe what happens at each step.

Bucket	Value
0
1
2
3
4
5
6
7
8
9

Long Answers

This semester we saw how different implementations of the priority queue ADT lead to different sorting algorithms. One that we didn't consider was binary search trees, which can be used as priority queues too. Consider the following sorting algorithm:
```
template <typename T>
void tree_sort(vector<T> &v) {
  binary_tree<T> t; // An unbalanced binary search tree
  // Insert all the elements of v into t.
  for (int i=0; i<v.size(); i++)
    t.insert(v[i]);
  // Perform an inorder traversal of t and write it into v.
  t.inorder_traversal(v);
}
```
1. What's the best-case and worst-case time complexity of this algorithm? Use big-O notation as a function of n, the number of values to be sorted.
  
  Best case:
  
  Worst case:
2. How might you improve the worst-case time complexity?
3. How much additional space (outside of v) does this algorithm use? Use big-O notation as a function of n.
4. Briefly, how should binary_tree::insert be implemented to make this sort stable?
5. Give one reason why you think this algorithm is no longer commonly used or taught.
You've been hired to develop a new navigation system for R2 droids (a fictional robot that can travel by ground as well as attach to a spaceship and travel by space). Given a starting point on one planet and a destination point possibly on another planet, it needs to give directions for the shortest path between the two points. Describe, at a high level, what data structures and algorithms you would use to implement such a system.

Make the following assumptions:
- Every planet has a system of roads, and the droid can't go off-road.
- Every planet has exactly one spaceport where the droid can get on/off a spaceship.
- Every planet has a fixed location, stored as (x,y,z) coordinates.
To achieve scalable performance, Map-Reduce relies on a distributed filesystem that replicates or copies files transparently to multiple machines. Normally, each chunk (fixed size block) is replicated at least 3 times to enable high availability. Write a function, fs_replication_check, which, given a vector of all the chunks in the file system, reports which chunks have fewer than replication_level duplicates:
```
void fs_replication_check(const vector<size_t> &all_chunks, size_t replication_level, vector<size_t> &bad_chunks) {
      // Returns: bad_chunks contains the chunk ids of all chunks in all_chunks
      //          which occur fewer than replication_level times.
      bad_chunks.clear();
```
Write a function to count how many connected components a graph has. For example, the following graph has three connected components:

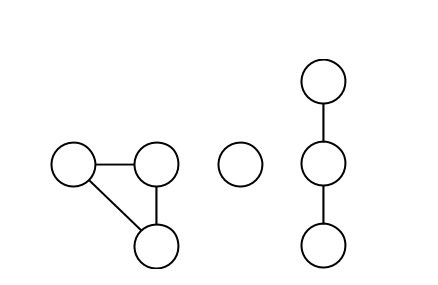
Assume that graphs are represented as adjacency lists, like this:
```
template <typename Node>
struct graph {
    unordered_set<Node> nodes;
    unordered_map<Node, unordered_set<Node>> edges;
};
```
Assume that the graph is undirected, so if there's an edge connecting u and v, then both edges[u].count(v) and edges[v].count(u) will be nonzero.

Hint: Remember that you can use either breadth-first search or depth-first search to traverse the nodes of a connected component.
```
template <typename Node>
int count_connected_components (const graph<Node> &g) {
    // Argument: g is an *undirected* graph, that is,
    // Returns: the number of connected components in g
```