Project 01: Arithmetic Scheme Interpreter

Overview

The first project is to build a simple arithmetic Scheme interpreter in C++. As a relative of Lisp, Scheme is a functional programming language with the unique property of homoiconicity, which means its syntax has the same structure as its abstract syntax tree.

Your arithmetic Scheme interpreter should do the following:

Read in a line of Scheme code from standard input, parse the text, and construct an abstract syntax tree.
Evaluate the abstract syntax tree by traversing it and simplifying expressions into a single value.
Display the result of the interpretation.

This project is to be done in groups of 1 - 3 and is due midnight Friday September 16, 2016.

Grammar

The Scheme dialect you must support has the following EBNF grammar:

<digit>         = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
<number>        = {<digit>}
<op>            = - | + | * | /
<expression>    = (<op> <expression> <expression>) | <number>

Given the above definition, note the following:

You only have to support natural numbers (i.e. 0, 1, 10, 100, ...).
You only have to support basic arithmetic operators: addition, subtraction, multiplication, and division.
You only have to support binary expressions (that is operations that take two arguments) or numeric literals.
You do not have to worry about syntax errors or invalid input. You can safely assume that any given test input will follow these rules.

A reference implementation of the arithmetic Scheme interpreter can be found at /afs/nd.edu/user15/pbui/pub/bin/uscheme. Here is an example transcript of its execution:

$ /afs/nd.edu/user15/pbui/pub/bin/uscheme -h
usage: /afs/nd.edu/user15/pbui/pub/uscheme
  -b Batch mode (disable prompt)
  -d Debug mode (display messages)

$ /afs/nd.edu/user15/pbui/pub/bin/uscheme
>>> 0
0
>>> 1
1
>>> (+ 1 2)
3
>>> (- 1 2)
-1
>>> (* 1 2)
2
>>> (/ 1 2)
0
>>> (+ (* 1 2) 1)
3
>>> (+ (* 2 3) (- 4 2))
8

To disable displaying the prompt, pass the -b flag to the uscheme program.

To enable displaying some debugging information, pass the -d flag to the uscheme program.

GitLab

To start this project, you must form a group of 1 - 3 people. One group member should fork the Project 01 repository on GitLab:

https://gitlab.com/nd-cse-30331-fa16/project01

Once this repository has been forked, follow the instructions from Reading 00 to:

Make the repository private
Configure access to the repository

Make sure you add all the members of the team in addition to the instructional staff.

As with the programming challenges in this course, the project repository contains a Makefile, input, and output test files for automated building and testing of your program.

In addition to these files, the repository should also contain the following:

measure.cpp: This is utility for measuring execution time and memory usage of an application.
uscheme.cpp: This is the first implementation of an arithmetic Scheme interpreter.
uschemeSmart.cpp: This is the second implementation of an arithmetic Scheme interpreter that uses smart pointers.

Structures

As noted above, our Scheme interpreter must read in a line of text from standard input and parse the data to form an abstract syntax tree that corresponds to the expression. For instance, given the expression (+ (+ 1 2) (+ 3 4)), we should form the following tree:

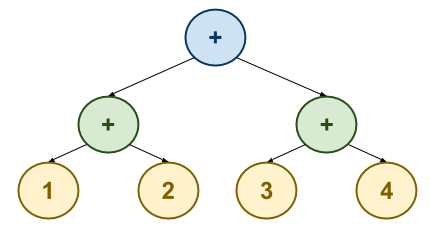
To represent our abstract syntax tree, we will use a binary tree structure:

struct Node:
    string value
    Node * left
    Node * right

You will need to complete the struct Node by implementing the constructor, the destructor, and the operator<< friend function whose purpose is to recursively print out the contents of the struct Node. For instance, the expression (+ (+ 1 2) (+ 3 4)) should yield the following output:

(Node: value=+, left=(Node: value=+, left=(Node: value=1), right=(Node: value=2)), right=(Node: value=+, left=(Node: value=3), right=(Node: value=4)))

Parser

The next step in implementing the Scheme interpreter is constructing a parser. While you may implement this any way you wish, the following is the recommended approach:

First, you will need a parse_token function whose purpose is to return the next token string from the input stream:
```
string parse_token(istream &s):
    Skip Whitespace

    if NextCharacter is a Parenthesis or NextCharacter is an OP:
        token = NextCharacter
    elif NextCharacter is a Digit:
        token = Read Number

    return token
```
This function first skips all leading whitespace. Next, it checks if the next character is a parenthesis or an arithmetic operator. If so, it sets the token to this character. If the next character is a digit, then it reads in the whole number and sets the token to this number. Finally, the function returns the token it found.

For instance, calling parse_token repeatedly on a stream with the contents (+ 1 2) should yield the following sequence of tokens:
```
(
+
1
2
)
```
Hints: To look at the next character from a stream, you can use the peek method. To perform the actual read, you can use the get method on the stream.

Second, you will need a parse_expression function whose purpose is to return the abstract syntax tree corresponding to an expression read from the input stream:

Node *parse_expression(istream &s):
      token = parse_token(s)

      if token is "" or token is ")":
          return nullptr

      if token is "(":
          token = parse_token(s)
          left  = parse_expression(s)
          if left:  right = parse_expression(s)
          if right: parse_token(s)

      return new Node(token, left, right)

This function recursively parses the input stream to build the abstract syntax tree.

Once you have completed all the components up to this point, you should be able to run the uscheme interpreter with the -d flag to examine the abstract syntax tree your parser is forming.

Interpreter

The final step to implementing the Scheme interpreter is to walk or traverse the abstract syntax tree you created. To do this, we will use a recursive strategy similar to a post-order depth first search:

void evaluate_r(const Node *n, stack<int> &s):
      Evaluate Node's Children
      Evaluate Node's Value

To evaluate the current value, we will simulate a stack machine. That is, if Value is a number, we simply push it onto the given stack s which represents the state of our machine. If Value is an arithmetic operation, we must pop off two operands from the stack s, perform the operation, and then push the result back onto the stack. This process repeats until the whole tree is traversed and there is one value remaining on the stack.

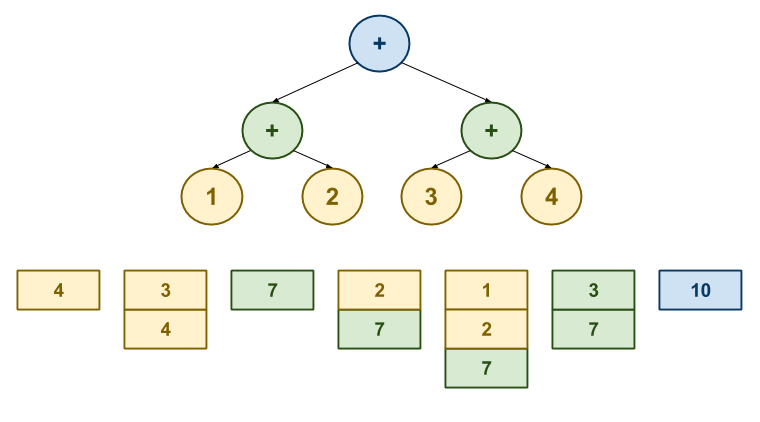
The diagram above shows the evolution of the stack as the interpreter traverses the abstract syntax tree from right to left for the expression (+ (+ 1 2) (+ 3 4)):

4 is pushed onto the stack.
3 is pushed onto the stack.
3 and 4 are popped and added together, and the resulting 7 is pushed onto the stack.
2 is pushed onto the stack.
1 is pushed onto the stack.
1 and 2 are popped and added together, and the resulting 3 is pushed onto the stack.
3 and 7 are popped and added together, and the resulting 10 is pushed onto the stack.

When the evaluation is complete, the final result of the expression will be on top of the stack s.

The purpose of the evaluate function is to call the evaluate_r function and return the result of the evaluation.

Smart Pointers

Once you have a working implementation of your Scheme interpreter (i.e. uscheme), you are to convert your existing program into a second version called uschemeSmart that utilizes smart pointers for memory management. In particular, you should use std::shared_ptr for references to nodes in the struct Node. Of course, you will need to modify other portions of the code to reflect this modification to complete the transformation.

Questions

When you are finished implementing your arithmetic Scheme interpreter, answer the following questions in the project01/README.md:

What is the complexity of your interpreter in terms of Big-O notation? Explain exactly what N is in this case and the asymptotic behavior of your interpreter for when N grows. Moreover, be sure to consider the impact of using a stack during evaluation.
Compare the resource usage of your two versions of the Scheme interpreter (i.e. uscheme and uschemeSmart) by determining:
- Which executable is larger?
- Which executable uses more memory?
Which implementation do you prefer: the one with manual memory management, or the one with smart pointers? Explain the trade-offs and your reasoning.
Real world Scheme interpreters such as Racket and Guile support arbitrary length expressions. For instance, instead of binary operations such as (+ 1 2), these implementations support (+ 1 2 3 4 5). What changes to your interpreter would you need to make support such syntax? Explain how the structures, parser, and interpreter would need to be modified.

In addition to the questions, please provide a brief summary of each individual group members contributions to the project.

Rubric

Your project will be scored based on the following metrics:

Metric	Points
`uscheme` passes output test	4
`uscheme` passes memory test	2
`uscheme` passes time test	1
`uschemeSmart` passes output test	4
`uschemeSmart` passes memory test	2
`uschemeSmart` passes time test	1
`README.md` responses	3
Coding Style	1
Individual contributions	2
Total	20

To test your programs, simply run make test. Your programs must correctly process the input correctly, have no memory errors, and run in the allotted time.

Submission

To submit your project, simply push your changes to your Project 01 repository. There is no need to create a Merge Request. Make sure you have enable access to your repository to all of the instructional staff.