Challenge 15: Maximum Concurrency

While working for Dr. Thain in the Cooperative Computing Lab, the instructor had to compose large scientific workflows that ran across many (ie. hundreds) of machines spread across the country in different compute clusters and data centers. To maximize the efficiency of these large scale computations, it was necessary to determine if there were any concurrent structures and thus opportunities for parallelization.

Fortunately, most scientific workflows involve composing many different utilities that perform a specialized task by taking the outputs of one program and using them as inputs to other utilities. One way to visualize such workflows is by forming a tree or DAG as shown below.

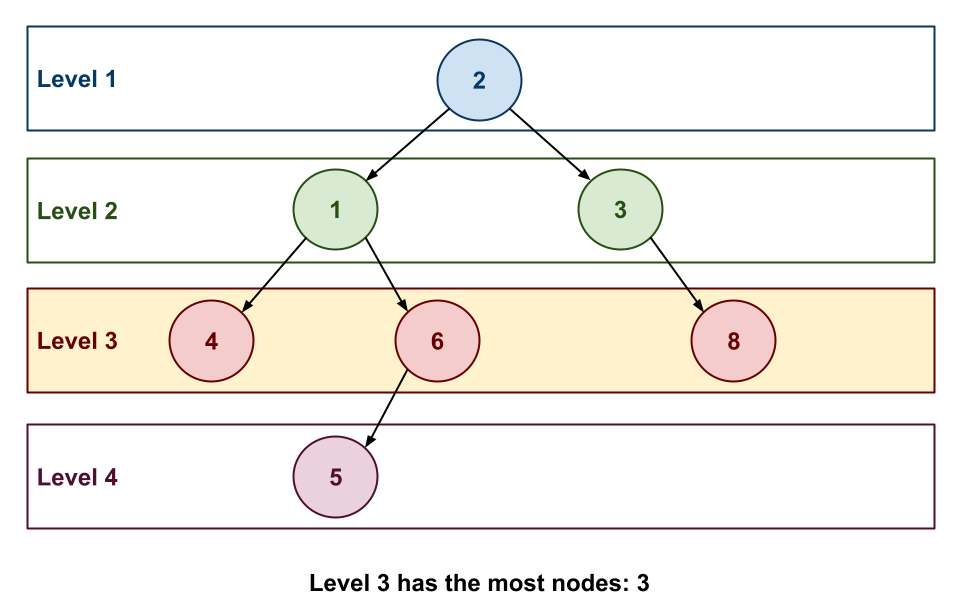
In the tree below, we have four levels of nodes:

1. Level 1: This has the root node and has a width of 1.

2. Level 2: This is the second level and has a width of 2 since it only has the nodes 1 and 3.

3. Level 3: This is the third level and has a width of 3 since it has the nodes 4, 6, and 8.

4. Level 4: This is the last level and has a with of 1.

As can be seen, the maximum width of this tree is 3. This means if that if we were to execute this workflow on multiple machines, then we could have a maximum of 3 concurrent tasks (and thus only need 3 different machines for maximum efficiency).

Since it has been a long time since the instructor has done anything related to distributed systems, your task is to read in workflows represented as binary trees and identify which level in each tree has the most nodes (and thus concurrency).

Input¶

You will be given a series of workflows represented by binary trees in pre-order traversal order.

Example Input¶

2 1 4 -1 -1 6 5 -1 -1 -1 3 -1 8 -1 -1

Note, the -1 in the input denotes that there is no Node there (ie. NULL).

Output¶

For each workflow, determine where it has its maximum concurrency by finding the level with the most nodes in the binary tree and output a message in the following format:

Level $MAX_LEVEL has the most nodes: $MAX_NODES

Example Output¶

Level 3 has the most nodes: 3

Note, if there are multiple levels with the maximum number of nodes, then choose the level with the highest value (ie. further down the tree).

Submission¶

To submit your work, follow the same procedure you used for Reading 01:

$ cd path/to/cse-34872-su21-assignments     # Go to assignments repository
$ git checkout master                       # Make sure we are on master
$ git pull --rebase                         # Pull any changes from GitHub

$ git checkout -b challenge15               # Create and checkout challenge15 branch

$ $EDITOR challenge15/program.cpp           # Edit your code

$ git add challenge15/program.cpp           # Stage your changes
$ git commit -m "challenge15: done"         # Commit your changes

$ git push -u origin challenge15            # Send changes to GitHub

To check your code, you can use the .scripts/check.py script or curl:

$ .scripts/check.py
Checking challenge15 program.cpp ...
  Result Success
    Time 0.03
   Score 6.00 / 6.00

$ curl -F source=@challenge15/program.cpp https://dredd.h4x0r.space/code/cse-34872-su21/challenge15
{"result": "Success", "score": 6, "time": 0.0319976806640625, "value": 6, "status": 0}