and Simple Examples.
Updated: Dec, 01, 1998
Aero - Optical
Effects: Motivations and Simple Examples.
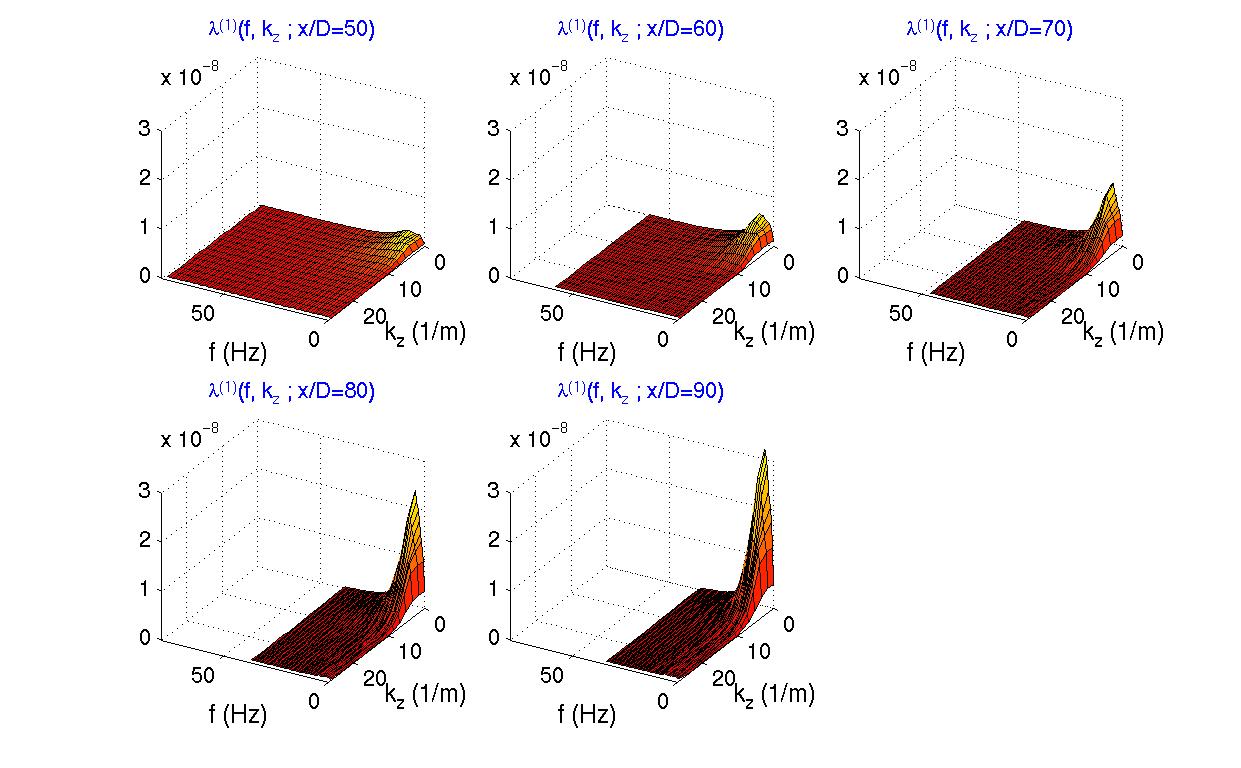
Unsteady aspects of the transition of a planar jet shear layer are investigated by application of a Morlet wavelet decomposition of the streamwise fluctuating velocity component. Because of its quasi-locality in both physical-space and Fourier-space, the wavelet transformation provides the unique capability for one to track the time evolution of the various scales in the flow. We focus upon unsteady aspects of the fundamental-subharmonic resonant phase locking and the simultaneous amplitude and phase modulations of the interacting fundamental and subharmonic instability waves. Of particular interest is the observation of intermittent fundamental-subharmonic phase locking. This intermittency is found to originate with the subharmonic instability which exhibits sudden pi-shifts in phase which coincide with deep drops in subharmonic amplitude. A fully nonlinear theoretical model based on the interaction between structures in the shear layer is developed in order to investigate the origin of these unsteady effects. The theoretical model is found to be in good agreement with experiment. The model is found to duplicate all the essential features of the unsteady behavior.
 . |
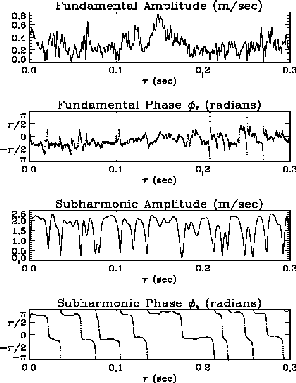Results are Obtained by Applying Morlet Wavelet Decomposition to a
Streamwise Velocity Component.
Jet: Two-dimensional acousticaly excited at f_fund=2500Hz with U0=20m/sec. Location of a Probe: x/theta=100, where theta is an initial thickness of the shear layer; y-location is at a local subharmonic maxima. |
See also Presentation
of Wavelet results on APS/DFD '96 meeting
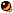Applications of Proper
Orthogonal Decomposition (POD) in Two-dimensional Jets.
Numerous experiments over the last several years have shown the existence of large-scale quasi-organized vortical structures in a variety of free and wall bounded turbulent flows. These so-called coherent structures appear to be dynamically important and play a key role in determining the macrocharacteristics of the flow such as mass, momentum and energy transport.
The Proper Orthogonal Decomposition (POD) was applied in a self-similar turbulent region of 2-D jet. It was found that pseudo-2-D vortex-like travelling structures exist in this region and they contain ~ 10\% of total kinetic energy of the flow. Many basic questions remain concerning the origin of the coherent structures, their evolution and mutual interaction.
Once a number of structures (modes) is extracted from
the turbulent flow, one can use them as basis functions and expand the
velocity field in series. Unlike standard mathematical basis functions,
the POD modes represent real statistical averaged structures which exist
in the flow. Once obtained, the Navier-Stocks equations can be reduced
to a finite number of ODE's. The theory of dynamical systems can be applied
to investigate the obtained system of ODE's
Specifically, the objective of the research will be to answer the following questions:
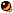Multi-point X-wire Measurements
in the Self-Similarity Region in the 2-D Jet: Investigation of the Existing
Large-Scale Structures.
Simultaneous two-component velocity measurements from two rake of several X-wire probes, located in the crosstream direction in planar turbulent jet at different streamwise stations have been taken. The experimental set-up is similar to the one by Ukeiley (Ukeiley, L., 'Dynamics of large scale structures in a plane turbulent mixing layer', Ph.D dissertation, Clarkson University, 1995 ) applied to a shear layer. Two-point cross-correlation tensor has been extracted. The tensor data has being used as input for different data-reduction techniques: POD, Wavelet transform in order to extract spatio-temporal evolution of the large-scale structures, existing in the flow.
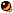Experimental
Facility and Measurements
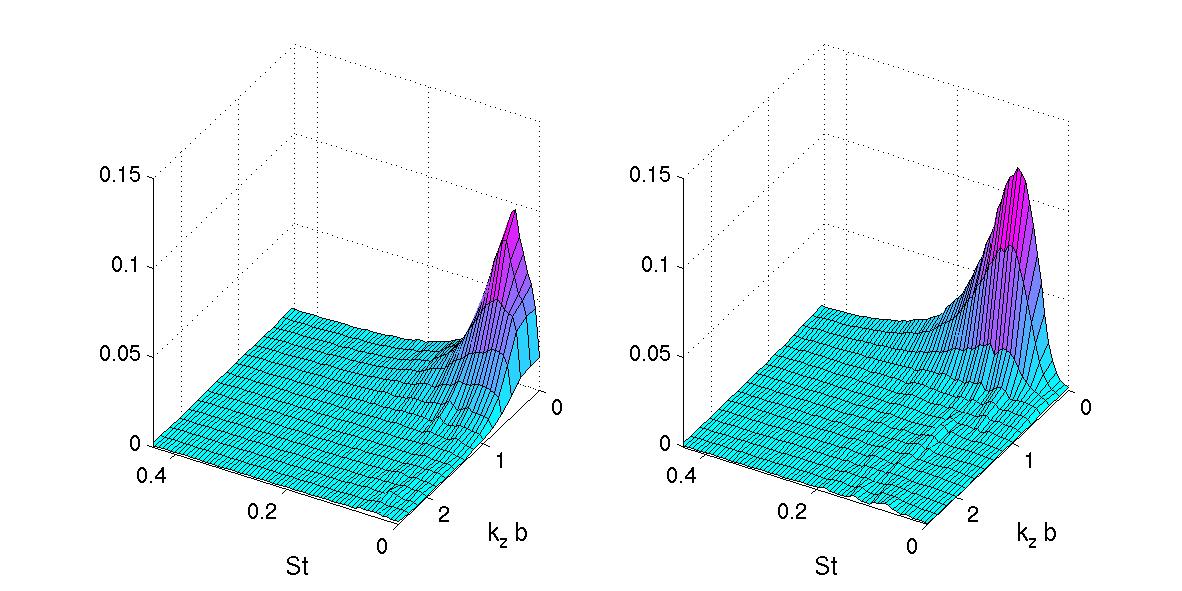
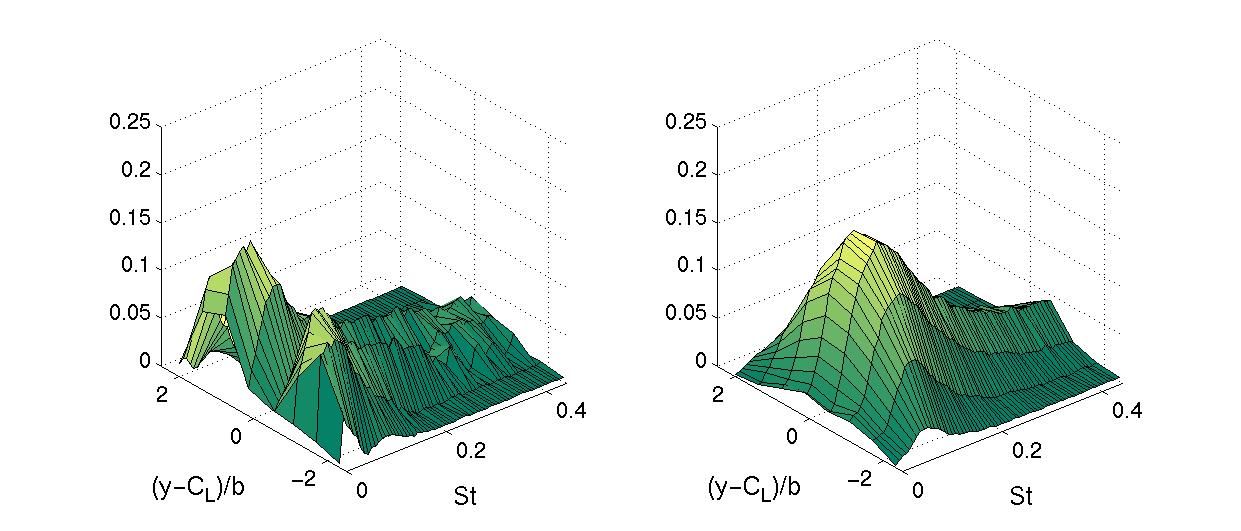
Some Selected Results
U-(left picture) and V-(right picture) Eigenvalues for
POD-Mode #1
