Homework 1: Inductive definitions and proofs

Due: 09/02 at 11:59pm
Points: 30

Please prepare your solutions as a PDF file (scanned handwriting is okay, but no .doc or .docx, please) and submit in Canvas.

1. Red-black trees: definition

In class, we saw a definition of binary trees whose nodes are labeled with integers.

Here’s a definition of binary trees whose nodes are colored either red or black. It defines a judgement t bintree that holds if and only if t is a binary tree with red or black nodes.

t₁ bintree   t₂ bintree
———————————————————————   c ∈ {red,black}
    c(t₁,t₂) bintree

       —————————          c ∈ {red,black}
       c bintree

Remember that we represent trees as symbolic expressions. For example, the tree drawn in Figure 1 is represented as black(red(black,black),black).

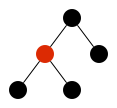
Write a definition of the judgement t rbtree that holds iff t is a binary tree whose colors satisfy the rules for red-black trees:

The root is black.
The leaves are black.
If a node is red, then both its children are black.
For each node, there is a number b (called its black-height) such that every path from the node to a leaf has exactly b black nodes.

Hint: First define the “helper” judgement t rbtree(c,b), which holds iff t is a red-black tree with root color c and black-height b. (For this “helper” judgement only, the requirement that the root is black is not enforced.) Then define t rbtree in terms of t rbtree(c,b).

Write a proof tree that shows that the tree shown in Figure 1 is a red-black tree.

2. Red-black trees: height bound

Define the height of a tree to be the maximum number of edges in a path from root to leaf. (Yes, it’s strange that black-height counts nodes but height counts edges.) You learned in Data Structures, but may not have proven, that the height of a red-black tree is O(log n), which makes them good for implementing dictionaries.

Prove, by induction(s) on the structure of derivations, that a red-black tree with n nodes has height at most 2 log₂ (n+1) − 2. Hint: Do this in three steps:

Prove that if t rbtree(c,b), then t has n ≥ 2^b − 1 nodes.
Prove that if t rbtree(c,b), then t has height h ≤ 2b − 1 if c is red, and h ≤ 2b − 2 if c is black.
Conclude that h ≤ 2 log₂ (n+1) − 2.

Note: This is the last time you will see a logarithm in this class!

3. Semantics of NB

Due on Monday 09/05 at 11:59pm

Using small-step semantics (with or without evaluation contexts – your choice), show that if iszero (pred (succ zero)) then false else true ⟶ if iszero zero then false else true.
Show that if iszero (pred (succ zero)) then false else true ⟶* false using a sequence of reductions, that is, fill in the ... below:
```
if iszero (pred (succ zero)) then false else true
⟶ if iszero zero then false else true
    ...
⟶ false
```
It’s enough to write the sequence of reductions; you don’t have to prove each step.
Using big-step semantics, show that if iszero (pred (succ zero)) then false else true ⇓ false (corrected 09/01)