Research projects

The diffuse interface method and applications to coupled systems in fluid dynamics
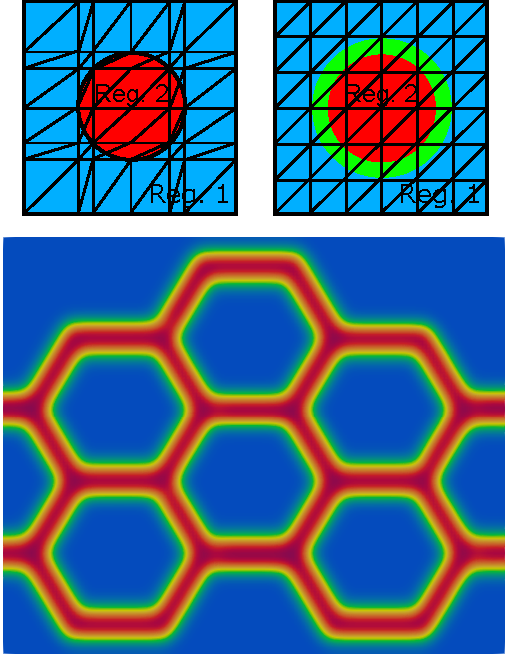
Coupled, moving domain problems, where a fluid interacts with a neighboring region, are often described using PDEs and coupling conditions that hold across a common interface. In order to accurately describe the interaction of the coupled problem, the interface tracking methods, in which mesh nodes are aligned with the parametric representation of the interface, are often used. However, interface-tracking methods rapidly become difficult to apply when mesh deformations are large. The diffuse interface method is an alternative strategy based on the fixed mesh approach, where the problem is reformulated using a phase-field function which smoothly transitions from zero in one region to one in the other region. This approach is useful even when the domain does not change in time, in cases where the interface between the two regions is difficult to determine exactly (e.g. "fuzzy" boundaries between regions obtained from medical images), or when the geometry of the interface is complex. However, the diffuse interface method introduces an additional error at the interface. The convergence and order of this term need to be carefully determined.
Development of adaptive, higher-order partitioned schemes for fluid-structure interaction problems
Fluid-structure interaction (FSI) problems arise in many applications, such as aerodynamics, and biomedical engineering. In realistic problems describing fluid flow, sometimes the dynamics are not known, or the variables are changing rapidly. Hence, robust adaptive time-stepping is central to accurate and efficient long-term predictions of the solution. This is particularly important in blood flow applications where the systolic part of the cycle exhibits significantly different dynamics from the dyastole. This study will contribute to the development of fast and efficient numerical schemes to solve FSI problems, which could be used in combination with non-invasive clinical measurement tools to provide an innovative approach to medical diagnosis and surgical decision making.
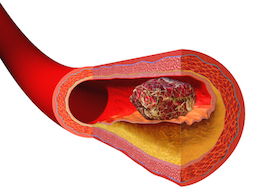
Quantification of the effects of blood clots on arterial blood flow
Thrombosis is associated with the formation of a blood clot inside of a blood vessel. Depending on the size and location of the blood clot, thrombosis may result in complete deprivation of oxygen, tissue death or stroke. Understanding the interaction between a blood clot, arterial wall and blood helps identify risk factors that might lead to medical complications, and is important for making decisions about medical treatment.
Modeling the interaction between poroelastic materials and fluid dynamics
The interaction of a free fluid with a deformable porous material occurs in many applications. In geomechanics, the extraction of oil and gas by fracking involves the interaction between a pressurized fluid and a surrounding soil. An example from biology is the perfusion of living tissues, where the fluid carried by the main vessels is distributed by filtration to the surrounding material. Our aim is to advance theoretical and computational models for fluid-poroelastic structure interaction problems.
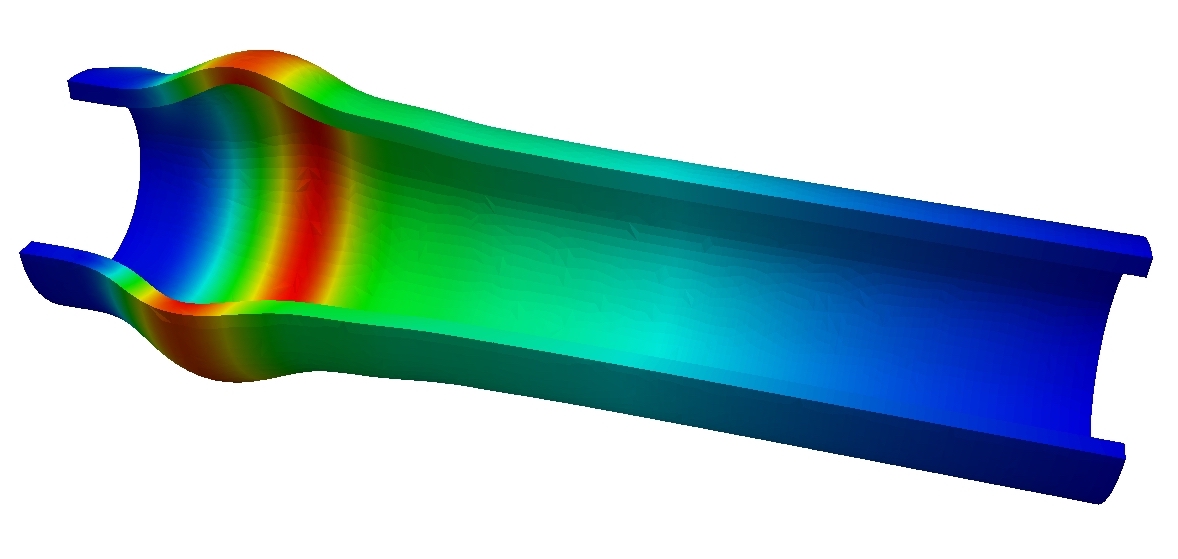
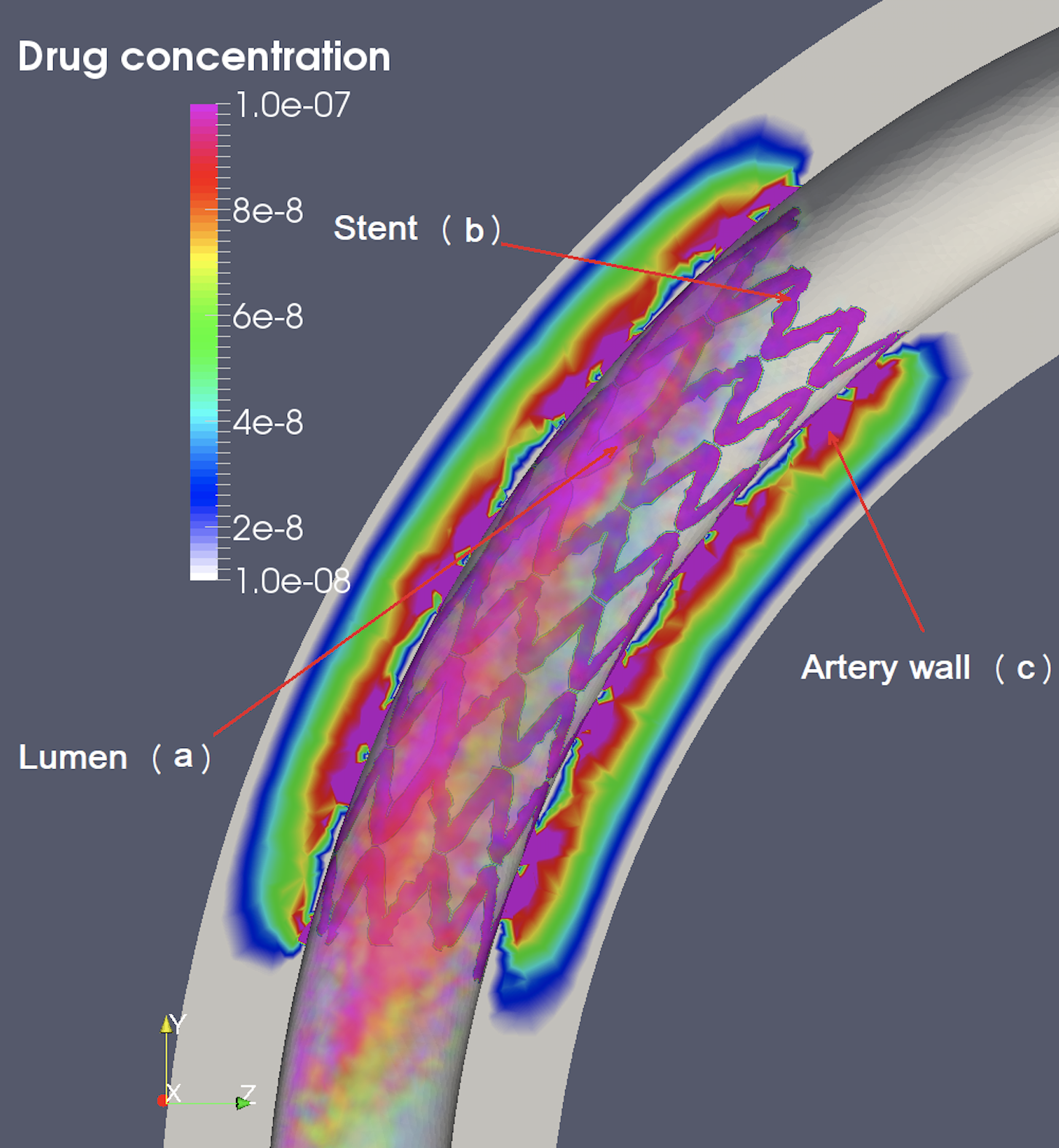
Modeling stents and their interaction with pulsatile blood flow in compliant vessels
A stent is a metallic mesh-like tube used to prop the clogged arteries open. Our focus is to study the performance of different stents (including biodegradable stents) inserted in a human artery and their response to the stresses exerted by blood flow and by the arterial tissue.