Many-Body Physics & Biology Group

Dervis Can Vural, Associate Professor. Physics Department, University of Notre Dame. Email: dvural@nd.edu, Room: Nieuwland Science Hall 384g

Introduction

We are a theoretical group interested in the collective behavior of physical and biological systems in which disorder and strong interactions play an important role. We specialize in statistical mechanics, soft condensed matter, evolutionary biology and ecology. We are particularly interested in questions surrounding the arrow of time, such as how materials and organisms fall apart, how evolution tangles ecological relationships, how our memory of the past fades, and how predicting the future relates to retrodicting the past. Below is a brief description of some of our recent work.

Aging, Failure and Death

aging Standard theories of aging typically focus on microscopic mechanisms such as oxidative damage or telomere shortening. However we age and die not because we run out of cells, but because small scale failures on the cellular level manifest at larger scales, leading to a macroscopic catastrophe.

We view aging as an emergent universal property of systems that consist of a large number of interdependent components (read). The video below shows how a large number of interdependent nodes fail.

Failure can also be viewed as a microscope that reveals the structure of a complex system. The failure times of components informs how they are interconnected. Read.

Recently, our experimental collaborators verified the interaction based picture of aging in synthetic tissues. Read.

Based on experimental observations and earlier theoretical ideas, we predict that tissues collapse through a wave of failure that propagates from outside inwards, with non-monotonic velocity. Read.

We organized a nice workshop surrounding these topics.

Disordered Materials

Materials such as glasses, polymers, disordered crystals, quasi-crystals and proteins lack long range order, and are thus referred as disordered solids. The standard model describing disordered solids at low temperatures postulate that these materials are composed of two level systems, i.e. atoms, or groups of atoms with two available discrete configurations.

Glass
All disordered solids universally exhibit certain properties which cannot be explained by the two level systems model. Here is a critique of the said model, and here is a more general model, from which the universality is derived.

Evolution of Cooperation

We develop physical models of evolutionary game theory to understand how cooperation emerges and persists despite the evolutionary incentive to cheat. Recently we discovered that flow shear enables and promotes social behavior in microbes. Specifically, shear tears apart social communities clusters, and thereby limiting the spread of cheating strains. The videos above shows how flow patterns can shape social evolution. In a vortex, cooperative microbes can sustain only within an annular region. In a flowing pipe, they can only sustain near the boundaries, where the shear is larger than a critical amount. Everywhere else cheaters take over, causing the groups to weaken and die. Read.

We also found that the physical characteristics such as diffusion lengths, flow patterns, and molecular decay rates play a significant role in governing whether a microbial community will evolve specialist or generalist forms of cooperation. Read.

Although cheating behavior is often devastating for social species, we have discovered that in special cases, cheating can, counterintuitively, benefit the community. This will happen, in the context of a disease or tumor, where rapid growth can be beneficial. Cheaters fueled by altruists will expand rapidly, and overwhelm the host immune system. Read.

Rewinding Randomness

Many astonishing facts about the origin of the universe, evolution of life, or history of civilizations will never be directly observed, but will only be inferred in the light of their manifestations in the present. Forward in time, any state of knowledge, regardless of how exact, will invariably deteriorate into an entropy maximizing probability distribution. We adresss the converse question: Given a measurement at present time, how rapidly does our knowledge fade away backwards in time? Read.

Theoretically relevant information such as original causes or underlying mechanisms are seldom directly observable. For example, one can easily measure the amount of proteins expressed in a cell but not necessarily know what interactions lead to the particular expression pattern. One can observe a certain species decline in numbers, but not exactly know which ecological relationship, or what triggering event causes the decline. When a virus spreads seemingly spontaneously, or when an invasive species expands its range, it is very difficult to know where it exactly came from, or its evolutionary trajectory that lead to its final success.

We develop algorithms and formulae to infer causal origins from raw empirical data, such as identifying the original trigerring event given an observed final state. Read.

Entropic Forces

When two macromolecules come very near each other in a fluid, the surrounding fluid molecules, having finite volume, are less likely to get in between. This causes the macromolecules to apprach each other as if attracted to one other. This entropic force is called depletion. Here we calculate the depletion force between linear disordered macromolecules. Read.

Slow Demons

A Maxwell's demon is a hypothetical device that opens and closes a gate separating two chambers filled with gas, based on its observations of approaching gas molecules. This way it sorts the atoms and reduces the entropy of the system. This thought experiment has been instrumental in establishing the connections between information, computation and thermodynamics for over a century.

Here we take into consideration the finite response time and finite size of the demon. For example, the gate cannot operate faster than the speed of light. These limitations establish theoretical upper limits toheat and mass transfer via local information processing. Read.

Ecological Evolution

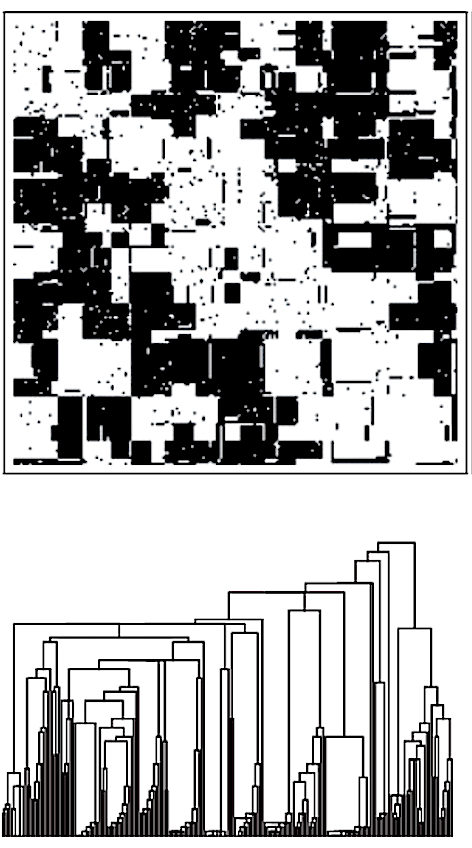
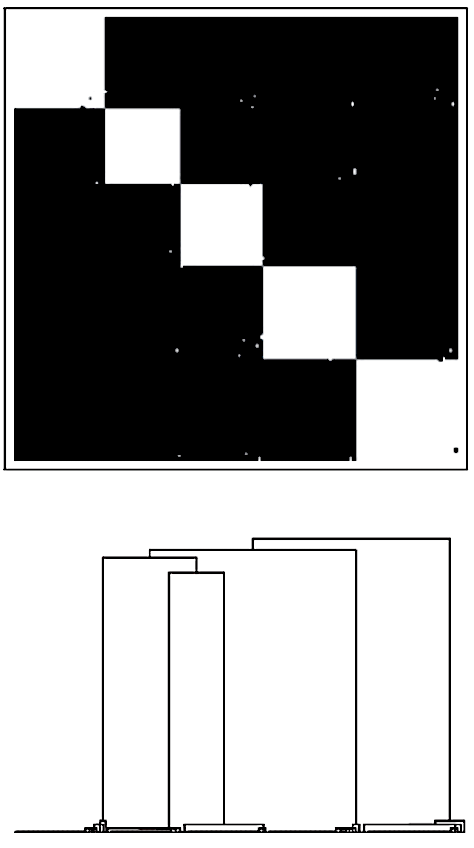
Start with a large number of unrelated species, put them together and wait for many generations. Eventually the interactions between them evolve into a tangled web of exchanges - so much, that no species can survive in isolation. Above are connectivity matrices and phylogenetic trees of two such communities subject to different selective pressures. Higher pressures (right) leads to the formation of specialized communities. Read.

Model Awareness

A model need not be a passive descriptor of its subject. If the subject is affected by the model building process, the model must be updated in real time. In some cases, the very act model building can cause the otherwise correct model to fail, or cause an otherwise incorrect model to succeed. In other cases, attempting to predict the future can be detrimental to the predictor. Read.

We studied the dynamics of a predictive swarm aiming to maximize the uptake of some resource. A predictive agent tries to estimate what others will do, and update its behavior accordingly. All other predictive agents are doing the same, trying to predict the trajectory of agents that are trying to predict them! The video above shows a few iterations o the thoughts of a predictor, while it says “they know that I know that they know that I know...". On the left, the resources are initialized randomly, whereas on the right resources are concentrated in two spots, one large and one small. Read.

Active Inference

Scientific inference involves obtaining the unknown properties or behavior of a system in the light of what is known, typically, without changing the system. We propose an alternative to this approach: a system can be modified in a targetted way, preferrably by a small amount, so that it becomes more predictable or more retrodictable. Read.

Quantization of Temperature

Temperature is conventionally defined in terms of the number of “possible" microstates, given a set of macroscopic constraints such as total energy or particle number. It is a remarkable that an information theoretical quantity can connect so well to physical observables, such as the hight of a mercury collumn, or the volume of a baloon.lead to its final success.

Here we offer an alternative view of temperature, and propose that temperature must be reformulated as a non-local non-realistic quantum variable. We demonstrate that if a large but finite system is split into two subsystems, their temperatures must get entangled. As such, an operator description of temperature becomes necessary to avoid an EPR-type causality violation. In this new picture, temperature is subject to the constraints of quantum mechanics, where its measurement must necessarily accompany a wavefunction collapse into a "temperature eigenstate". Read.